Introduction#
The capacity of a road is typically expressed as vehicles/hour and describes the maximum traffic flow that a road can handle.
As a rule of thumb, the capacity of a multi-lane road is the product of the capacity of a single lane multiplied by the number of lanes. The exact relationship is more complex and depends on the distribution of vehicle speeds and the lane changing dynamics.
Lane Capacity#
The capacity of a single lane is inversely proportional to time headways between successive vehicles. Assuming homogeneous traffic and equal headways:
capacity = 3600 / grossTimeHeadway
Where grossTimeHeadway denotes the time it takes for two successive vehicle
front-bumpers to pass the same location.
In contrast netTimeHeadway denotes the time it takes for the follower vehicles
front-bumper to reach the location of the leaders rear-bumper.
Computing Headways#
The exact time headways observed in the simulation depend on the used carFollowModel and its parameters. The easiest case to analyze is the one where all vehicles drive at the same speed s.
Let grossHeadway denote the distance between successive vehicle front-bumpers
and netHeadway denote the distance from follower front-bumper to leader
rear-bumper.
For the default 'Krauss'-Model, the following vType attributes are relevant for the minimum time headway (corresponding to maximum flow and hence lane capacity):
- length: the physical length of a vehicle in m (default 5)
- minGap: the minimum gap between vehicles in a standing queue in m (default 2.5)
- tau: the desired minimum time headway in seconds (default 1)
Assuming that all vehicles are driving at at constant speed s, the following headways hold for 'Krauss':
netHeadway = minGap + tau * sgrossHeadway = length + minGap + tau * s
From this we can directly compute the time headways:
netTimeHeadway = minGap / s + taugrossTimeHeadway = (length + minGap) / s + tau
Due to length and minGap, the capacity of a road depends on its speed limit (whereas the tau component is independent of speed). At high road speeds, the tau component is the dominant factor whereas length and minGap dominate at low speeds.
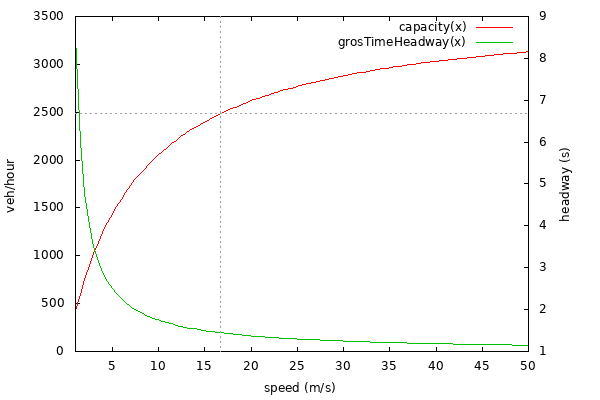
The following graph shows the ideal time headways and road capacities for different road speeds with the default model parameters for length, minGap and tau.
Further headway effects#
The above computation only holds for vehicles driving at constant speeds and with minimum distances. This rarely occurs in a simulation for the following reasons
- vehicles have different desired speeds (modeled as a speedFactor distribution)
- vehicles have randomized slow-downs (depending on the carFollowModel).
- vehicles are not always in a configuration of minimum following distances. Care must be taken especially for vehicle insertion
The following table shows road capacities that can be achieved at vehicle insertion depending on the used vType and insertion parameters. The road speed limit was 16.66m/s which gives a theoretical capacity of 2482 veh/hour. The script which produces the data points for the table below can be found here.
| sigma | speedDev | departSpeed | capacity | capacity --step-length 0.1 |
capacity --extrapolate-departpos |
capacity --step-length 0.1 --extrapolate-departpos |
|---|---|---|---|---|---|---|
| 0.5 | 0.1 | 0 | 1198 | 1368 | 1198 | 1368 |
| 0.5 | 0.1 | max | 1635 | 2183 | 1653 | 2186 |
| 0.5 | 0.1 | desired | 1522 | 2052 | 1921 | 2090 |
| 0.5 | 0.1 | avg | 1933 | 2206 | 1974 | 2211 |
| 0.5 | 0 | 0 | 1200 | 1368 | 1200 | 1368 |
| 0.5 | 0 | max | 1643 | 2188 | 1664 | 2188 |
| 0.5 | 0 | desired | 1800 | 2400 | 2128 | 2441 |
| 0.5 | 0 | avg | 1800 | 2400 | 2142 | 2446 |
| 0 | 0.1 | 0 | 1440 | 1500 | 1440 | 1500 |
| 0 | 0.1 | max | 2075 | 2276 | 2087 | 2276 |
| 0 | 0.1 | desired | 1663 | 2080 | 2190 | 2183 |
| 0 | 0.1 | avg | 2199 | 2238 | 2235 | 2243 |
| 0 | 0 | 0 | 1440 | 1500 | 1440 | 1500 |
| 0 | 0 | max | 2073 | 2489 | 2083 | 2489 |
| 0 | 0 | desired | 1800 | 2400 | 2482 | 2483 |
| 0 | 0 | avg | 1800 | 2400 | 2482 | 2483 |
Comments
- default departSpeed is '0' which gives the worst possible insertion capacity
- default sigma is '0.5' and default speedDev for passenger cars is 0.1
- for the default Krauss model, step-length has a side effect on the average speed reduction from sigma (this can be remedied by setting
sigmaStep="1"in thevType)
Insertion capacity on a 2-lane road#
The following table shows road capacities that can be achieved at vehicle insertion on a 2-lane road depending on the used insertion parameters. The road speed limit was 16.66m/s which gives a theoretical capacity of 4964 veh/hour. The script which produces the data points for the table below can be found here.
- sigma was constant at 0.5
- speedDev was constant at 0.1
| departLane | departSpeed | capacity | capacity --step-length 0.1 |
capacity --extrapolate-departpos |
capacity --step-length 0.1 --extrapolate-departpos |
|---|---|---|---|---|---|
| first | max | 1664 | 3224 | 1657 | 3210 |
| random | max | 3289 | 4370 | 3298 | 4376 |
| free | max | 3279 | 4378 | 3304 | 4379 |
| best_prob | max | 3331 | 4419 | 3321 | 4432 |
| first | avg | 1922 | 2653 | 2385 | 2763 |
| random | avg | 3881 | 4421 | 3972 | 4426 |
| free | avg | 3870 | 4432 | 3970 | 4431 |
| best_prob | avg | 3878 | 4500 | 4039 | 4512 |
Insertion capacity on a 3-lane road#
The following table shows road capacities that can be achieved at vehicle insertion on a 3-lane road depending on the used insertion parameters. The road speed limit was 16.66m/s which gives a theoretical capacity of 7447 veh/hour. The script which produces the data points for the table below can be found here.
- sigma was constant at 0.5
- speedDev was constant at 0.1
| departLane | departSpeed | capacity | capacity --step-length 0.1 |
capacity --extrapolate-departpos |
capacity --step-length 0.1 --extrapolate-departpos |
|---|---|---|---|---|---|
| first | max | 1647 | 3216 | 1656 | 3224 |
| random | max | 4952 | 6569 | 4953 | 6575 |
| free | max | 4936 | 6568 | 4956 | 6562 |
| best_prob | max | 5068 | 6683 | 5053 | 6706 |
| first | avg | 1907 | 2623 | 2369 | 2708 |
| random | avg | 5826 | 6626 | 5958 | 6639 |
| free | avg | 5794 | 6641 | 5951 | 6659 |
| best_prob | avg | 5718 | 6845 | 6136 | 6854 |
