• Road Capacity
Road Capacity

Introduction#

The capacity of a road is typically expressed as vehicles/hour and describes the maximum traffic flow that a road can handle.

As a rule of thumb, the capacity of a multi-lane road is the product of the capacity of a single lane multiplied by the number of lanes. The exact relationship is more complex and depends on the distribution of vehicle speeds and the lane changing dynamics.

Lane Capacity#

The capacity of a single lane is inversely proportional to time headways between successive vehicles. Assuming homogeneous traffic and equal headways:

capacity = 3600 / grossTimeHeadway

Where grossTimeHeadway denotes the time it takes for two successive vehicle front-bumpers to pass the same location.

In contrast netTimeHeadway denotes the time it takes for the follower vehicles front-bumper to reach the location of the leaders rear-bumper.

Computing Headways#

The exact time headways observed in the simulation depend on the used carFollowModel and its parameters. The easiest case to analyze is the one where all vehicles drive at the same speed s.

Let grossHeadway denote the distance between successive vehicle front-bumpers and netHeadway denote the distance from follower front-bumper to leader rear-bumper.

For the default 'Krauss'-Model, the following vType attributes are relevant for the minimum time headway (corresponding to maximum flow and hence lane capacity):

  • length: the physical length of a vehicle in m (default 5)
  • minGap: the minimum gap between vehicles in a standing queue in m (default 2.5)
  • tau: the desired minimum time headway in seconds (default 1)

Assuming that all vehicles are driving at at constant speed s, the following headways hold for 'Krauss':

  • netHeadway = minGap + tau * s
  • grossHeadway = length + minGap + tau * s

From this we can directly compute the time headways:

  • netTimeHeadway = minGap / s + tau
  • grossTimeHeadway = (length + minGap) / s + tau

Due to length and minGap, the capacity of a road depends on its speed limit (whereas the tau component is independent of speed). At high road speeds, the tau component is the dominant factor whereas length and minGap dominate at low speeds.

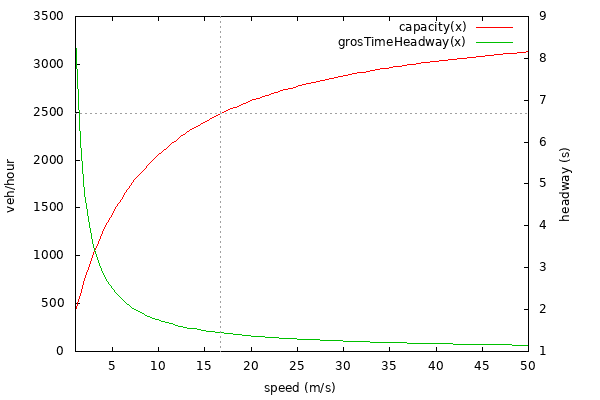
The following graph shows the ideal time headways and road capacities for different road speeds with the default model parameters for length, minGap and tau.

capacity.png

Further headway effects#

The above computation only holds for vehicles driving at constant speeds and with minimum distances. This rarely occurs in a simulation for the following reasons

The following table shows road capacities that can be achieved at vehicle insertion depending on the used vType and insertion parameters. The road speed limit was 16.66m/s which gives a theoretical capacity of 2482 veh/hour. The script which produces the data points for the table below can be found here.

sigma speedDev departSpeed capacity capacity
--step-length 0.1		 capacity
--extrapolate-departpos		 capacity
--step-length 0.1
--extrapolate-departpos
0.5 0.1 0 1198 1368 1198 1368
0.5 0.1 max 1635 2183 1653 2186
0.5 0.1 desired 1522 2052 1921 2090
0.5 0.1 avg 1933 2206 1974 2211
0.5 0 0 1200 1368 1200 1368
0.5 0 max 1643 2188 1664 2188
0.5 0 desired 1800 2400 2128 2441
0.5 0 avg 1800 2400 2142 2446
0 0.1 0 1440 1500 1440 1500
0 0.1 max 2075 2276 2087 2276
0 0.1 desired 1663 2080 2190 2183
0 0.1 avg 2199 2238 2235 2243
0 0 0 1440 1500 1440 1500
0 0 max 2073 2489 2083 2489
0 0 desired 1800 2400 2482 2483
0 0 avg 1800 2400 2482 2483

Comments

  • default departSpeed is '0' which gives the worst possible insertion capacity
  • default sigma is '0.5' and default speedDev for passenger cars is 0.1
  • for the default Krauss model, step-length has a side effect on the average speed reduction from sigma (this can be remedied by setting sigmaStep="1" in the vType)

Insertion capacity on a 2-lane road#

The following table shows road capacities that can be achieved at vehicle insertion on a 2-lane road depending on the used insertion parameters. The road speed limit was 16.66m/s which gives a theoretical capacity of 4964 veh/hour. The script which produces the data points for the table below can be found here.

  • sigma was constant at 0.5
  • speedDev was constant at 0.1
departLane departSpeed capacity capacity
--step-length 0.1		 capacity
--extrapolate-departpos		 capacity
--step-length 0.1
--extrapolate-departpos
first max 1664 3224 1657 3210
random max 3289 4370 3298 4376
free max 3279 4378 3304 4379
best_prob max 3331 4419 3321 4432
first avg 1922 2653 2385 2763
random avg 3881 4421 3972 4426
free avg 3870 4432 3970 4431
best_prob avg 3878 4500 4039 4512

Insertion capacity on a 3-lane road#

The following table shows road capacities that can be achieved at vehicle insertion on a 3-lane road depending on the used insertion parameters. The road speed limit was 16.66m/s which gives a theoretical capacity of 7447 veh/hour. The script which produces the data points for the table below can be found here.

  • sigma was constant at 0.5
  • speedDev was constant at 0.1
departLane departSpeed capacity capacity
--step-length 0.1		 capacity
--extrapolate-departpos		 capacity
--step-length 0.1
--extrapolate-departpos
first max 1647 3216 1656 3224
random max 4952 6569 4953 6575
free max 4936 6568 4956 6562
best_prob max 5068 6683 5053 6706
first avg 1907 2623 2369 2708
random avg 5826 6626 5958 6639
free avg 5794 6641 5951 6659
best_prob avg 5718 6845 6136 6854